Phong là một nhà điêu khắc, ông có một tấm đá cẩm thạch hình chữ nhật kích thước W × H. Ông ta muốn cắt tấm đá thành các miếng hình chữ nhật kích thước W1 × H1, W2 × H2, . . . , WN × HN. Ông ta muốn cắt đến tối đa các mẫu kích thước có thể. Tấm đá có những vân đá cho nên không thể xoay khi sử dụng, có nghĩa là không thể cắt ra miếng B × A thay cho miếng A × B trừ khi A = B. Các miếng phải được cắt tại các điểm nguyên trên hàng cột và mỗi nhát cắt phải cắt đến hết hàng hoặc hết cột. Sau khi cắt sẽ còn lại những mẩu đá còn thừa bỏ đi, nghĩa là những mẩu đá không thể cắt thành miếng kích thước cho trước nào.
Yêu cầu: Hãy tìm cách cắt sao cho còn ít nhất diện tích đá thừa bỏ đi.
Dữ liệu vào
Dòng đầu tiên chứa hai số nguyên: W và H.
Dòng thứ hai chứa một số nguyên N.
N dòng tiếp theo mỗi dòng chứa hai số nguyên Wi và Hi.
Kết quả
Ghi ra duy nhất một số nguyên là tổng diện tích nhỏ nhất các miếng thừa bỏ đi.
Ví dụ
Input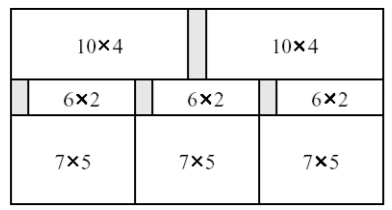
21 11
4
10 4
6 2
7 5
15 10
Output
10
Giới hạn:
• 1 ≤ W ≤ 600, 1 ≤ H ≤ 600, 0 < N ≤ 200, 1 ≤ Wi ≤ W, and 1 ≤ Hi ≤ H.
• Có 50% số test ứng với W ≤ 20, H ≤ 20 và N ≤ 5.
Nguồn: ĐPT 20172018
- Caytao - Caytao
- chiendau - chiendau
- catdayso - catdayso
- 23dnab4 - Rút tiền (THTB Đà Nẵng 2023)
- 23dnab3 - Bộ ba số (THTB Đà Nẵng 2023)
- 23dnab2 - Trung bình cộng (THTB Đà Nẵng 2023) Bài 2
- 23dnab1 - Chuẩn hóa (THTB Đà Nẵng 2023) Bài 1
- 23strb4 - Không tiếp đất (THTB Sơn Trà, Đà Nẵng 2023) Bài 4
- 23strb3 - Trò chơi lớn (THTB Sơn Trà, Đà Nẵng 2023) Bài 3
- 23strb2 - Nhảy dân vũ (THTB Sơn Trà, Đà Nẵng 2023) Bài 2