Cho lưới ô vuông kích thước n dòng và n cột. Các dòng của lưới được đánh số từ 1 đến n. Các cột của lưới cũng được đánh số từ 1 đến n. Ô nằm trên giao của dòng i và cột j của lưới được gọi là ô (i,j) và (i,j) được gọi là tọa độ của nó. Mỗi ô của lưới chứa một số thuộc tập {0, 1}. Ô chứa số 0 được gọi là ô tự do còn ô chứa số 1 được gọi là ô bị cản. Robot được đặt ở ô (L1, C1) cần phải di chuyển đến ô (L2, C2). Robot chỉ có thể di chuyển theo hướng thẳng đứng hoặc hướng nằm ngang.
Yêu cầu: Cần xác định:
1) Số lần đổi hướng ít nhất để robot có thể di chuyển từ ô (L1, C1) tới ô (L2, C2).
2) Số lần đổi hướng ít nhất để robot có thể di chuyển từ ô (L1, C1) tới ô (L2, C2) trong tình huống được phép biến một ô bị cản thành ô tự do.
3) Số lượng các ô bị cản mà việc loại bỏ bất cứ một ô nào trong số chúng, ta đều đạt được số lần đổi hướng như trong câu 2).
Dữ liệu
- Dòng thứ nhất chứa số nguyên n, 1<=n<=1000;
- n dòng tiếp theo, mỗi dòng chứa n số 0 hoặc 1 được ghi cách nhau bởi dấu cách mô tả trạng thái của lưới
- Dòng thứ n+2 chứa 4 số L1, C1,L2, C2 (đảm bảo là các ô (L1, C1) và ô (L2, C2) là các ô tự do).
Kết quả:
Ghi ra ba số nguyên là các câu trả lời cho 3 yêu cầu tương ứng nêu trong đầu bài
Ví dụ
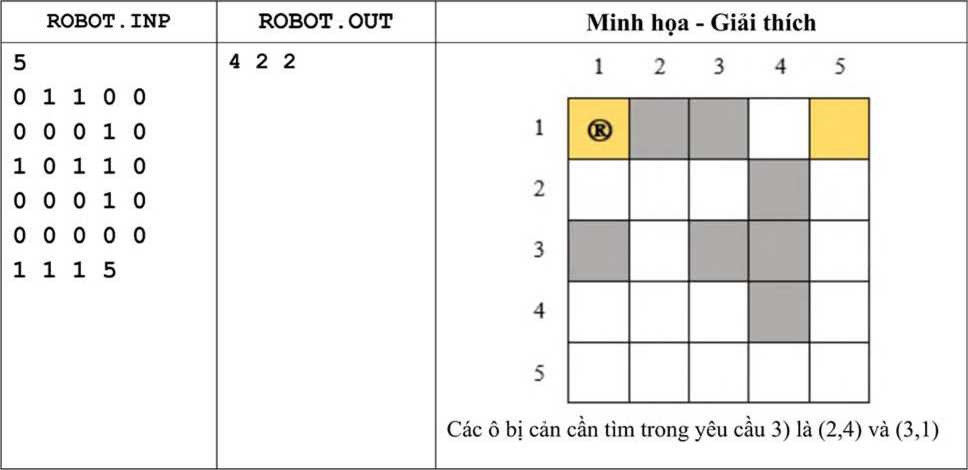
Nguồn: NĐN 20172018
- Caytao - Caytao
- chiendau - chiendau
- catdayso - catdayso
- 23dnab4 - Rút tiền (THTB Đà Nẵng 2023)
- 23dnab3 - Bộ ba số (THTB Đà Nẵng 2023)
- 23dnab2 - Trung bình cộng (THTB Đà Nẵng 2023) Bài 2
- 23dnab1 - Chuẩn hóa (THTB Đà Nẵng 2023) Bài 1
- 23strb4 - Không tiếp đất (THTB Sơn Trà, Đà Nẵng 2023) Bài 4
- 23strb3 - Trò chơi lớn (THTB Sơn Trà, Đà Nẵng 2023) Bài 3
- 23strb2 - Nhảy dân vũ (THTB Sơn Trà, Đà Nẵng 2023) Bài 2