Thành vẽ một cây (đồ thị vô hướng liên thông không có chu trình) với N nút được đánh số từ 1 đến N và muốn tô màu các nút của cây bằng màu đen hoặc trắng. Trên cây, hai nút có thể ghép đôi với nhau khi và chỉ khi chúng thỏa mãn các điều kiện sau:
• cả hai cùng được tô bởi màu trắng, và
• hoặc là có cạnh nối trực tiếp giữa chúng hoặc là có thể nối chúng bởi một đường đi đơn chỉ gồm toàn nút màu đen ngoại trừ hai nút đầu mút là màu trắng.
Yêu cầu: hãy giúp Thành tô màu các nút của cây bằng màu đen hoặc trắng sao cho số lượng cặp nút có thể ghép đôi với nhau là lớn nhất.
Dữ liệu vào
Dòng đầu tiên chứa một số nguyên dương T (T ≤ 10) là số lượng bộ test, mỗi bộ test chứa thông tin về một cây cần tô màu có cấu trúc như sau:
• Dòng thứ nhất chứa một số nguyên dương N (N ≤ 5000) là số lượng nút của cây;
• Mỗi dòng trong số N − 1 dòng tiếp theo chứa hai số nguyên x, y cách nhau bởi dấu cách cho biết có cạnh nối trực tiếp giữa hai nút x và y.
Kết quả
Ghi ra T dòng, mỗi dòng một số nguyên là kết quả tìm được tương ứng với các bộ test trong dữ liệu vào.
Ví dụ
Input
2 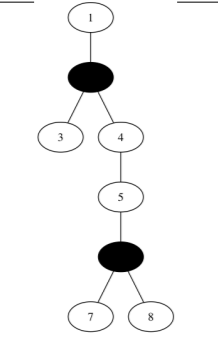
8
1 2
2 3
2 4
4 5
5 6
6 7
6 8
2
1 2
Output
7
1
Giải thích
Có 2 bộ test trong dữ liệu vào (T = 2).
Đối với bộ test thứ nhất, cây có 8 nút và 7 cạnh, trong hình vẽ (hình ở trên) là cách tô màu cho số lượng cặp nút có thể ghép đôi là lớn nhất (7 cặp). Các cặp đó là: (1, 3), (1, 4), (3, 4), (4, 5), (5, 7) (5, 8), (7, 8).
Đối với bộ test thứ hai, cây chỉ có 2 nút và được nối với nhau bởi một cạnh duy nhất. Vì vậy cần tô cả 2 nút đó bằng màu trắng và tạo ra duy nhất một cặp nút có thể ghép đôi.
Nguồn: ĐPT '1819
- Caytao - Caytao
- chiendau - chiendau
- catdayso - catdayso
- 23dnab4 - Rút tiền (THTB Đà Nẵng 2023)
- 23dnab3 - Bộ ba số (THTB Đà Nẵng 2023)
- 23dnab2 - Trung bình cộng (THTB Đà Nẵng 2023) Bài 2
- 23dnab1 - Chuẩn hóa (THTB Đà Nẵng 2023) Bài 1
- 23strb4 - Không tiếp đất (THTB Sơn Trà, Đà Nẵng 2023) Bài 4
- 23strb3 - Trò chơi lớn (THTB Sơn Trà, Đà Nẵng 2023) Bài 3
- 23strb2 - Nhảy dân vũ (THTB Sơn Trà, Đà Nẵng 2023) Bài 2