An sống ở thành phố XYZ, hàng ngày anh phải đi làm từ nhà tới cơ quan bằng xe buýt. Thành phố XYZ có n nút giao thông được đánh số từ 1 đến n và m tuyến xe buýt hai chiều. Mỗi cặp nút giao thông i, j có không quá một tuyến xe buýt hai chiều, nếu có thì để đi từ nút i đến nút j (hoặc từ nút j đến nút i) với giá vé là cij=cji đồng. Vị trí nhà An nằm ở nút giao thông 1 còn cơ quan nằm ở nút giao thông n. Để lựa chọn đường đi từ nhà đến cơ quan An luôn chọn theo đường đi với chi phí ít nhất.
|
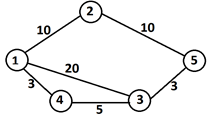
Ví dụ: thành phố có 5 nút giao thông và 6 tuyến xe buýt: Đường đi 1 -> 4 -> 3 -> 5 hết 11 đồng là ít nhất. |
|
Vừa qua An nhận được một vé đi xe buýt miễn phí. Vé có thể dùng để đi xe buýt miễn phí một lần trên một tuyến bất kỳ. Với vé xe miễn phí này An muốn biết chi phí ít nhất để đi từ nhà đến cơ quan là bao nhiêu.
Với ví dụ trên, đường đi 1 -> 3 -> 5 có sử dụng vé xe miễn phí (tại tuyến 1-3) hết 3 đồng là ít nhất.
Yêu cầu: Cho biết các tuyến xe buýt và giá vé tương ứng. Hãy tìm chi phí ít nhất để đi từ nhà (nút giao thông 1) đến cơ quan (nút giao thông n) với vé xe miễn phí mà An có.
Dữ liệu vào
- Dòng đầu tiên ghi hai số nguyên dương n và m (3<=n<=5000)
- m dòng sau, mỗi dòng 3 số nguyên i, j, cij (1 <= i, j <=n, 0<=cij <=30000) mô tả có tuyến xe buýt i -> j hết cij đồng.
Hai số liên tiếp trên một dòng cách nhau một dấu cách. Dữ liệu bảo đảm luôn có đường đi từ 1 đến n.
Kết quả
Ghi ra một số duy nhất là chi phí ít nhất để đi từ nhà (nút giao thông 1) đến cơ quan (nút giao thông n) với vé xe miễn phí mà An có.
Ví dụ
Input
5 6
1 2 10
2 5 10
1 4 3
3 4 5
3 5 3
1 3 20
Output
3
Input
5 5
1 2 10
2 5 10
1 4 3
4 3 5
3 5 3
Output
6
Nguồn: 3D '1819
- Caytao - Caytao
- chiendau - chiendau
- catdayso - catdayso
- 23dnab4 - Rút tiền (THTB Đà Nẵng 2023)
- 23dnab3 - Bộ ba số (THTB Đà Nẵng 2023)
- 23dnab2 - Trung bình cộng (THTB Đà Nẵng 2023) Bài 2
- 23dnab1 - Chuẩn hóa (THTB Đà Nẵng 2023) Bài 1
- 23strb4 - Không tiếp đất (THTB Sơn Trà, Đà Nẵng 2023) Bài 4
- 23strb3 - Trò chơi lớn (THTB Sơn Trà, Đà Nẵng 2023) Bài 3
- 23strb2 - Nhảy dân vũ (THTB Sơn Trà, Đà Nẵng 2023) Bài 2