Lưu ý : Bài này chỉ khác phiên bản dễ ở cấu trúc của dữ liệu, và giới hạn của giá trị ai
Ami có một cái cây (đơn đồ thị vô hướng liên thông không chu trình) có n nút. Các nút được đánh số từ 1. Trên các nút của cây có các giá trị, giá trị trên nút i là vi. Đường đi từ nút u đến v là một dãy a1, a2, a3, ..., at thoả mãn các điều kiện sau :
1) a1 = u và at = v
2) Đường đi là ngắn nhất giữa 2 đỉnh u và v
3) Với mọi i < t, có cạnh nối trực tiếp giữa ai và ai+1.
Các bạn cần tính xem có bao nhiêu giá trị D ≥ 0 mà tồn tại ít nhất một đường đi giữa 2 nút u và v bất kỳ trên cây là một cấp số cộng với công sai D. Với mỗi D ≥ 0 tìm được, hãy tìm xem đường đi dài nhất thoả mãn điều kiện đó.
Input
Dòng đầu tiên gồm một số nguyên dương n (n ≤ 3*105) là số đỉnh của cây.
N-1 dòng tiếp theo, mỗi dòng chứa 2 số u và v (u , v ≤ n), biểu diễn một cạnh nối giữa 2 đỉnh u và v.
Dòng tiếp theo gồm n số nguyên a1, a2, a3, ..., an (|ai| ≤ 109). Ai là giá trị trên nút i.
Output
Gồm một vài dòng, mỗi dòng có 2 số D x. Với ý nghĩa, đường đi dài nhất có công sai D có độ dài là x.
Các bạn cần in D theo thứ tự tăng dần.
Ví dụ
-
input9
1 2
1 3
2 4
2 5
3 6
3 7
5 8
7 9
1 4 0 3 7 -1 -1 10 -2output1 4
3 4
Giải thích
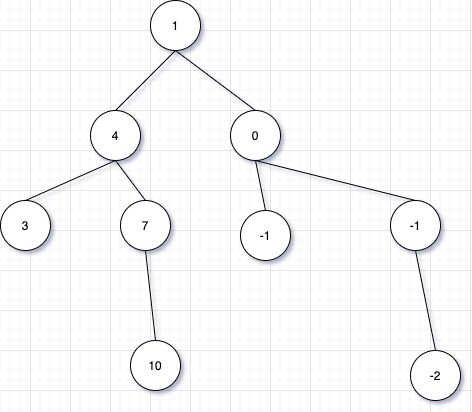
Một đường đi có công sai 1 là đường đi từ nút 9 đến 1. Dãy số là -2 -1 0 1 và có độ dài là 4
Một đường đi có công sai 3 là đường đi từ nút 1 đến nút 8. Dãy số là 1 4 7 10 và có độ dài là 4.
- Caytao - Caytao
- chiendau - chiendau
- catdayso - catdayso
- 23dnab4 - Rút tiền (THTB Đà Nẵng 2023)
- 23dnab3 - Bộ ba số (THTB Đà Nẵng 2023)
- 23dnab2 - Trung bình cộng (THTB Đà Nẵng 2023) Bài 2
- 23dnab1 - Chuẩn hóa (THTB Đà Nẵng 2023) Bài 1
- 23strb4 - Không tiếp đất (THTB Sơn Trà, Đà Nẵng 2023) Bài 4
- 23strb3 - Trò chơi lớn (THTB Sơn Trà, Đà Nẵng 2023) Bài 3
- 23strb2 - Nhảy dân vũ (THTB Sơn Trà, Đà Nẵng 2023) Bài 2